题目内容
15. 如图,直角△ABC中,∠ACB=90°,把△ABC绕点C旋转到△DCE,当DC经过AB的中点M时,求证:DE∥BC.
如图,直角△ABC中,∠ACB=90°,把△ABC绕点C旋转到△DCE,当DC经过AB的中点M时,求证:DE∥BC.
分析 先根据直角三角形斜边上的中线性质得到CM=BM=AM,则∠B=∠MCB,再根据旋转的性质得∠B=∠D,所以∠D=∠MCB,然后根据平行线的判定即可得到结论.
解答 证明:∵点M为直角△ABC斜边AB的中点,
∴CM=BM=AM,
∴∠B=∠MCB,
∵△ABC绕点C旋转到△DCE,
∴∠B=∠D,
∴∠D=∠MCB,
∴DE∥BC.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
3.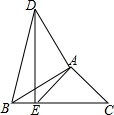 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
10.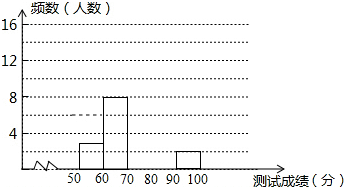 为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)求表中m的值;
(2)请把频数分布直方图补充完整;
(3)第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导,则第4组的小王与小李能同时抽到的概率是多少?
 为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 7 |
| 第3组 | 70≤x<80 | 10 |
| 第4组 | 80≤x<90 | m |
| 第5组 | 90≤x<100 | 2 |
(2)请把频数分布直方图补充完整;
(3)第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导,则第4组的小王与小李能同时抽到的概率是多少?
4.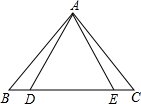 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )
 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )| A. | AB=AC | B. | ∠BAE=∠CAD | C. | BE=DC | D. | AD=DE |
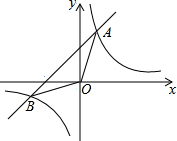 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交反比例函数y=$\frac{k}{x}$的图象于另一点B.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交反比例函数y=$\frac{k}{x}$的图象于另一点B.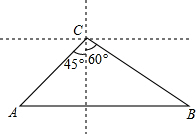 如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)
如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)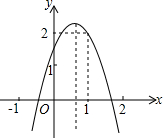 如图,已知二次函数y=ax2+bx+c(a≠0)的图形经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:①abc<0;②a<b<-2a;③b2+8a<4ac;④-1<a<0.其中正确结论的序号是①②.
如图,已知二次函数y=ax2+bx+c(a≠0)的图形经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:①abc<0;②a<b<-2a;③b2+8a<4ac;④-1<a<0.其中正确结论的序号是①②.