题目内容
6.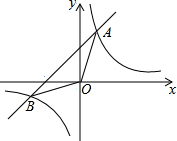 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交反比例函数y=$\frac{k}{x}$的图象于另一点B.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交反比例函数y=$\frac{k}{x}$的图象于另一点B.(1)求k和b的值;
(2)求△OAB的面积.
分析 (1)只需把点A的坐标代入一次函数和反比例函数的解析式,就可解决问题;
(2)只需求出直线AB与y轴的交点,然后运用割补法就可解决问题.
解答 解:(1)∵点A(2,5)是直线y=x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点,
∴5=2+b,k=2×5=10,
∴b=3,
即k和b的值分别为10、3;
(2)解方程组$\left\{\begin{array}{l}{y=\frac{10}{x}}\\{y=x+3}\end{array}\right.$,得
$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-5}\\{{y}_{2}=-2}\end{array}\right.$
∴点B(-5,-2).
∵点C是直线y=x+3与y轴的交点,
∴点C(0,3),
∴S△OAB=S△OAC+S△OBC
=$\frac{1}{2}$×3×2+$\frac{1}{2}$×3×5=$\frac{21}{2}$,
即△OAB的面积为$\frac{21}{2}$.
点评 本题主要考查了直线与反比例函数图象上点的坐标特征、运用待定系数法求直线与反比例函数的解析式、解方程组等知识,运用割补法是解决第(2)小题的关键.

练习册系列答案
相关题目
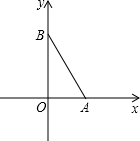 如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.
如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.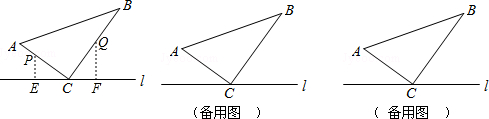
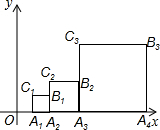 如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0). 如图,直角△ABC中,∠ACB=90°,把△ABC绕点C旋转到△DCE,当DC经过AB的中点M时,求证:DE∥BC.
如图,直角△ABC中,∠ACB=90°,把△ABC绕点C旋转到△DCE,当DC经过AB的中点M时,求证:DE∥BC.