题目内容
4.解下列不等式(组),并把解集用数轴表示出来.(1)5(x-2)>4(2x-1)
(2)$\frac{x-1}{2}+1≥\frac{x}{4}$
(3)$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$
(4)$\left\{\begin{array}{l}{1+2x>3+x}\\{5x≤4x-1}\end{array}\right.$.
分析 (1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得;
(3)分别求出每一个不等式的解集,将两个不等式解集表示在数轴上,找到其公共部分,从而确定不等式组的解集;
(4)分别求出每一个不等式的解集,将两个不等式解集表示在数轴上,找到其公共部分,从而确定不等式组的解集.
解答 解:(1)去括号,得:5x-10>8x-4,
移项,得:5x-8x>-4+10,
合并同类项,得:-3x>6,
系数化为1,得:x<-2,
将解集表示在数轴上如下所示: ;
;
(2)去分母,得:2(x-1)+4≥x,
去括号,得:2x-2+4≥x,
移项,得:2x-x≥2-4,
合并同类项,得:x≥-2,
将不等式解集表示在数轴上如下图所示: ;
;
(3)解不等式x-3(x-2)≥4,得:x≤1,
解不等式$\frac{1+2x}{3}$>x-1,得:x<4,
将不等式解集表示在数轴上如下图所示:
故不等式组的解集为:x≤1;
(4)解不等式:1+2x>3+x,得:x>2,
解不等式5x≤4x-1得:x≤-1,
将不等式解集表示在数轴上如下图所示:
故不等式组无解.
点评 本题主要考查解一元一次不等式(组)的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变,不等式组解集可借助数轴确定公共部分或根据口诀也可确定.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
12.下列关于平角和周角的说法正确的是( )
| A. | 平角是一条线段 | B. | 周角是一条射线 | ||
| C. | 两个锐角的和不一定小于平角 | D. | 反向延长射线OA,就形成一个平角 |
16.计算2$\sqrt{\frac{1}{2}}$$+3\sqrt{\frac{1}{3}}$$-\sqrt{8}$的结果是( )
| A. | $\sqrt{3}-\sqrt{2}$ | B. | $\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{2}$ |
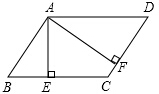 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.
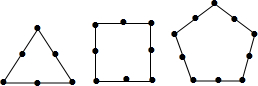 墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.
墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子. 如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.
如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.