题目内容
14. 如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.
如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.
分析 由正方形的性质得出AD=CD,∠EAD=∠BCD=∠FCD=90°,由SAS证明△ADE≌△CDF,得出对应边相等即可.
解答 证明:∵四边形ABCD是正方形,
∴AD=CD,∠EAD=∠BCD=90°,
∴∠FCD=90°,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠FCD=90°}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF(SAS),
∴DE=DF.
点评 此题主要考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.等腰三角形的一个外角等于130°,则这个等腰三角形的底角为( )
| A. | 65° | B. | 50° | C. | 65°或40° | D. | 50°或65° |
 如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=2.4cm.
如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=2.4cm.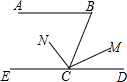 如图,已知AB∥CD,CN是∠BCE的平分线.
如图,已知AB∥CD,CN是∠BCE的平分线.
 墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )
墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( ) 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.
如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.