题目内容
14.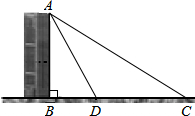 如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.
如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.
分析 在Rt△ABC中,设AB=x,则AC=2x,BC=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,在Rt△ABD中,$\frac{x}{\sqrt{3}x-20}$=tan60°,据此即可求出AB的长.
解答 解:在Rt△ABC中,设AB=x,则AC=2x,BC=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,
则BD=($\sqrt{3}$x-20)米,
在Rt△ABD中,$\frac{x}{\sqrt{3}x-20}$=tan60°,
$\frac{x}{\sqrt{3}x-20}$=$\sqrt{3}$,
∴x=10$\sqrt{3}$.
答:楼AB的高为10$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
5.在△ABC和△A′B′C′中,若AB=A′B′,∠B=∠B′,补充下列哪一个条件后仍不能判定△ABC与△A′B′C全等( )
| A. | BC=B′C′ | B. | ∠A=∠A′ | C. | ∠C=∠C′ | D. | AC=A′C′ |
9.目前我县在校学生约为21600名,21600用科学记数法表示正确的是( )
| A. | 2.16×103 | B. | 21.6×103 | C. | 0.216×104 | D. | 2.16×104 |
19.已知m,n是方程x2+2x-5=0的两个实数根,则m2-mn+3m+n=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
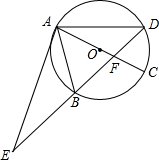 如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.