题目内容
18.计算:(1)$\sqrt{4}$-(3-$\sqrt{2}$)0+($\frac{1}{3}$)-2;
(2)(a-$\frac{1}{a}$)+$\frac{{a}^{2}-2a+1}{a}$.
分析 (1)直接利用零指数幂的性质以及负整数指数幂的性质和算术平方根的性质化简求出即可;
(2)首先将括号里面通分进而去括号化简求出即可.
解答 解:(1)$\sqrt{4}$-(3-$\sqrt{2}$)0+($\frac{1}{3}$)-2
=2-1+9
=10;
(2)(a-$\frac{1}{a}$)+$\frac{{a}^{2}-2a+1}{a}$
=$\frac{{a}^{2}-1}{a}$+$\frac{{a}^{2}-2a+1}{a}$
=$\frac{2{a}^{2}-2a}{a}$
=2a-2.
点评 此题主要考查了分式的混合运算以及实数运算,正确进行分式通分运算是解题关键.

练习册系列答案
相关题目
9.目前我县在校学生约为21600名,21600用科学记数法表示正确的是( )
| A. | 2.16×103 | B. | 21.6×103 | C. | 0.216×104 | D. | 2.16×104 |
7.在下列代数式中,次数为3的单项式是( )
| A. | x3+y3 | B. | xy2 | C. | x3y | D. | 3xy |
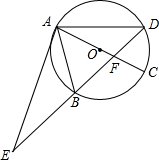 如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.