题目内容
5．计算：$\sqrt{12}$×（$\sqrt{3}$$-\sqrt{\frac{1}{3}}$）分析 首先利用单项式与多项式的乘法，然后进行化简即可．
解答 解：原式=$\sqrt{36}$-$\sqrt{4}$=6-2=4．
点评 本题考查的是二次根式的混合运算，在进行此类运算时，一定要把二次根式化为最简二次根式的形式．
练习册系列答案
相关题目
如图，某校A位于工地O的正西方向，且OA=200m，一辆红岩大货车从O点出发，以每秒10米的速度沿北偏西53°方向行驶，已知货车的噪声污染半径为130m，则学校受噪声污染的时间为10秒．（已知sin53°=0.80，tan37°=0.75）
13．
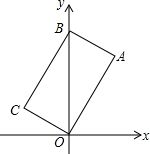矩形OABC在如图所示的平面直角坐标系中，点B的坐标是（0，2），∠AOB=30°，则点C的坐标是（ ）
矩形OABC在如图所示的平面直角坐标系中，点B的坐标是（0，2），∠AOB=30°，则点C的坐标是（ ）| A． | （-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$） | B． | （-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | C． | （-$\sqrt{3}$，1） | D． | （-1，$\sqrt{3}$） |
20．下列计算正确的是（ ）
| A． | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | B． | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C． | 4$\sqrt{3}$-3$\sqrt{3}$=1 | D． | 3+2$\sqrt{2}$=5$\sqrt{2}$ |
15．下列方程一定是一元二次方程的是（ ）
| A． | 3x2+$\frac{2}{x}$-1=0 | B． | 5x2-6y-3=0 | C． | ax2-x+2=0 | D． | 3x2=2x |