题目内容
已知△ABC的周长是20,三边分别为a、b、c,
(1)若b是最大边,求b的取值范围;
(2)若△ABC是不等边三角形,b是最大边,c是最小边,且b=3c,a、b、c均为整数,求△ABC的三边长.
(1)若b是最大边,求b的取值范围;
(2)若△ABC是不等边三角形,b是最大边,c是最小边,且b=3c,a、b、c均为整数,求△ABC的三边长.
考点:三角形三边关系
专题:
分析:(1)根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边即可求解.三角形的任意两边的和大于第三边,已知三边和周长,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;
(2)根据(1)中求出的b的取值范围,结合b为整数,得出b=7,8,9,又b=3c,c为整数,得出b=9,c=3,然后根据△ABC的周长是20求出a的长.
(2)根据(1)中求出的b的取值范围,结合b为整数,得出b=7,8,9,又b=3c,c为整数,得出b=9,c=3,然后根据△ABC的周长是20求出a的长.
解答:解:(1)依题意有b≥a,b≥c,又a+c>b,
则a+b+c≤3b且a+b+c>2b,
得2b<20≤3b,
得
≤b<10;
(2)∵
≤b<10,b为整数,
∴b=7,8,9,
∵b=3c,c为整数,
∴b=9,c=3,
∴a=20-b-c=8.
故△ABC的三边长为c=3,a=8,b=9.
则a+b+c≤3b且a+b+c>2b,
得2b<20≤3b,
得
| 20 |
| 3 |
(2)∵
| 20 |
| 3 |
∴b=7,8,9,
∵b=3c,c为整数,
∴b=9,c=3,
∴a=20-b-c=8.
故△ABC的三边长为c=3,a=8,b=9.
点评:本题考查了三角形三边关系,根据三角形三边关系定理列出不等式,求出b的取值范围是解题的关键.

练习册系列答案
相关题目
实数a、b在数轴上对应点的位置如图,则|a-b|-
的结果是( ) 
| a2 |

| A、2a-b | B、b-2a |
| C、b | D、-b |
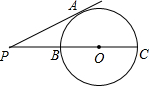 如图,已知PA切⊙O于点A,直线PBC经过圆心,PA=4,PB=2,则sin∠P=
如图,已知PA切⊙O于点A,直线PBC经过圆心,PA=4,PB=2,则sin∠P=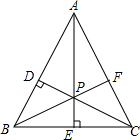 如图,△ABC边AB、BC的垂直平分线交于点P.
如图,△ABC边AB、BC的垂直平分线交于点P.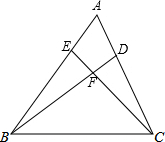 在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE.
在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE.