题目内容
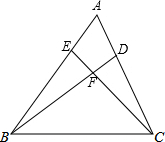 在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE.
在△ABC中,D、E分别在AC、AB上,且满足∠ABD=∠ACE.(1)找出图中存在的相似三角形,并简述理由;
(2)若将已知∠ABD=∠ACE改为“BD⊥AC,CE⊥AB,垂足分别为D、E”,图中存在几对相似三角形?请一一写出.
考点:相似三角形的判定
专题:
分析:(1)由∠ABD=∠ACE,∠A是公共角,∠EFB=∠DFC(对顶角相等),即可判定△ABD∽△ACE,△BEF∽△CDF;
(2)由BD⊥AC,CE⊥AB,可得∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,又由∠A=∠A,∠EFB=∠DFC,即可判定△AEC∽△ADB,△BEF∽△CDF.
(2)由BD⊥AC,CE⊥AB,可得∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,又由∠A=∠A,∠EFB=∠DFC,即可判定△AEC∽△ADB,△BEF∽△CDF.
解答:解:(1)∵∠ABD=∠ACE,∠A是公共角,
∴△ABD∽△ACE,
∵∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)两对.
∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF.
∴△ABD∽△ACE,
∵∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)两对.
∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF.
点评:此题考查了相似三角形的判定.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,圆锥的侧面积为8πcm2,母线与底面夹角为60°,则此圆锥的高为( )
如图,圆锥的侧面积为8πcm2,母线与底面夹角为60°,则此圆锥的高为( )| A、4cm | ||
| B、8cm | ||
C、2
| ||
| D、6cm |
 画出如图立体图形的三视图.
画出如图立体图形的三视图. 有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|=
有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|=