题目内容
17．
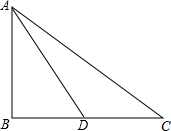如果一个三角形一边上的中线长恰好等于这边的长，那么这个三角形称为“有趣三角形”，这条中线称为“有趣中线”．如图，已知Rt△ABC中，∠B=90°，若Rt△ABC是“有趣三角形”，AD为“有趣中线”，且AD=14cm，则AC=9$\sqrt{3}$cm．
分析 根据题意得出DB的长，再利用勾股定理得出AB，AC的长．
解答 解：由题意可得：AD=BC=14cm，
则BD=7cm，
故在Rt△ABD中，AB=$\sqrt{1{4}^{2}-{7}^{2}}$=7$\sqrt{3}$（cm），
在Rt△ABC中，AC=$\sqrt{1{4}^{2}+（7\sqrt{3}）^{2}}$=9$\sqrt{3}$（cm）．
故答案为：9$\sqrt{3}$．
点评 此题主要考查了勾股定理的应用，根据题意得出AB的长是解题关键．
练习册系列答案
相关题目
7．一次函数y=2x+3的图象不经过的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
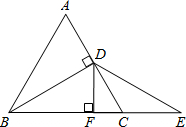△ABC是等边三角形，BD是AC边上的高，延长BC到E，使CE=CD，过点D作DF⊥BE于F．探究FC与BE间的数量关系，并证明．