题目内容
 如图,直线y=-
如图,直线y=-| 1 |
| 2 |
| k |
| x |
考点:反比例函数综合题,勾股定理,相似三角形的判定与性质
专题:计算题
分析:由点A在直线y=-
x上可得到AC=2OC,由∠COB=∠A可得到△OCB∽△ACO,从而得到
=
,进而可以得到OC=2BC,也就有AB=AC-BC=3BC,OB2=BC2+OC2=5BC2.由条件AB2-OB2=4就可得到BC的值,从而得到OC的值,就可求出k的值.
| 1 |
| 2 |
| OC |
| AC |
| CB |
| CO |
解答:解:设点A的坐标为(a,b),
则有AC=-a,OC=b.
∵点A在直线y=-
x上,
∴b=-
a即a=-2b.
∴AC=2OC.
∵∠COB=∠A,∠OCB=∠ACO,
∴△OCB∽△ACO.
∴
=
.
∴CO=2CB.
∴AC=2OC=4BC.
∴AB=3BC.
∵AC∥x轴,x轴⊥y轴,
∴AC⊥y轴.
∴OB2=BC2+OC2=BC2+(2BC)2=5BC2.
∵AB2-OB2=4,
∴(3BC)2-5BC2=4.
解得:BC=1.
∴OC=2.
∴点B的坐标为(-1,2).
∵点B在双曲线y=
(k≠0)上,
∴k=-1×2=-2.
故答案为:-2.
则有AC=-a,OC=b.
∵点A在直线y=-
| 1 |
| 2 |
∴b=-
| 1 |
| 2 |
∴AC=2OC.

∵∠COB=∠A,∠OCB=∠ACO,
∴△OCB∽△ACO.
∴
| OC |
| AC |
| CB |
| CO |
∴CO=2CB.
∴AC=2OC=4BC.
∴AB=3BC.
∵AC∥x轴,x轴⊥y轴,
∴AC⊥y轴.
∴OB2=BC2+OC2=BC2+(2BC)2=5BC2.
∵AB2-OB2=4,
∴(3BC)2-5BC2=4.
解得:BC=1.
∴OC=2.
∴点B的坐标为(-1,2).
∵点B在双曲线y=
| k |
| x |
∴k=-1×2=-2.
故答案为:-2.
点评:本题考查了反比例图象上点的坐标特征、相似三角形的判定与性质、勾股定理等知识,而找到AB、OB与BC之间的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
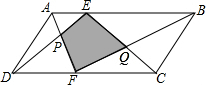 如图,E、F是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15cm2,S△BOC=25cm2,则阴影部分的面积为
如图,E、F是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15cm2,S△BOC=25cm2,则阴影部分的面积为 矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=
矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=