题目内容
 矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=
矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=| 8 |
| x |
| k |
| x |
考点:反比例函数综合题
专题:
分析:先根据OA=4,OC=6,点D在双曲线y=
上求出D点的坐标,再由DG∥OA得出G点纵坐标,设出G、E两点坐标,根据∠EGD=∠EDG即可得出EG=ED,再根据GE两点共线可得出G点坐标,代入双曲线y=
(k>0)即可得出k的值.
| 8 |
| x |
| k |
| x |
解答:解:∵矩形OABC中OA=4,
∴直线AB的解析式为x=4,
∵点D在双曲线y=
上,
∴D(4,2),
∵DG∥OA,
∴设G(a,2),E(b,6),
∵∠EGD=∠EDG,
∴点E在线段GD的垂直平分线上,
∴
=b①,
设直线OG的解析式为y=cx(c≠0),
∵点G、E均在直线上,
∴2=ca,6=cb,
∴
=
②,
①②联立得,a=
,
∴G(
,2),
∵点G在双曲线y=
(k>0)上,
∴k=
×2=
.
故答案为:
.
∴直线AB的解析式为x=4,
∵点D在双曲线y=
| 8 |
| x |
∴D(4,2),
∵DG∥OA,
∴设G(a,2),E(b,6),
∵∠EGD=∠EDG,
∴点E在线段GD的垂直平分线上,
∴
| a+4 |
| 2 |
设直线OG的解析式为y=cx(c≠0),
∵点G、E均在直线上,
∴2=ca,6=cb,
∴
| a |
| b |
| 1 |
| 3 |
①②联立得,a=
| 4 |
| 5 |
∴G(
| 4 |
| 5 |
∵点G在双曲线y=
| k |
| x |
∴k=
| 4 |
| 5 |
| 8 |
| 5 |
故答案为:
| 8 |
| 5 |
点评:本题考查的是反比例函数综合题,涉及到矩形的性质、反比例函数图象上点的坐标特点等知识,难度适中.

练习册系列答案
相关题目
若不等式(a-2)x>a-2的解集为x>1,那么字母a的取值范围是( )
| A、a>1 | B、a<1 |
| C、a>2 | D、a<2 |
 如图,直线y=-
如图,直线y=-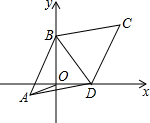 如图,已知菱形ABCD中,BC=10,∠BCD=60°两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是
如图,已知菱形ABCD中,BC=10,∠BCD=60°两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 如图,梯形ABCD中,AD∥BC,点E在BC上,AE∥CD,AD=10cm,梯形ABCD的周长为60cm,则△ABE的周长为
如图,梯形ABCD中,AD∥BC,点E在BC上,AE∥CD,AD=10cm,梯形ABCD的周长为60cm,则△ABE的周长为 如图,已知∠1=∠2,则图中互相平行的线段是
如图,已知∠1=∠2,则图中互相平行的线段是