题目内容
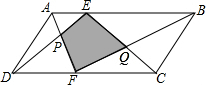如图，E、F是平行四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q．若S△APD=15cm2，S△BOC=25cm2，则阴影部分的面积为考点：平行四边形的性质
专题：
分析：作出辅助线EF，因为△ADF与△DEF同底等高，所以面积相等，所以阴影图形的面积可解．
解答：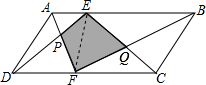
解：如图，连接EF
∵△ADF与△DEF同底等高，
∴S△ADF=S△DEF，
即S△ADF-S△DPF=S△DEF-S△DPF，
即S△APD=S△EPF=15cm2，
同理可得S△BQC=S△EFQ=25cm2，
∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2．
故答案为40．
解：如图，连接EF∵△ADF与△DEF同底等高，
∴S△ADF=S△DEF，
即S△ADF-S△DPF=S△DEF-S△DPF，
即S△APD=S△EPF=15cm2，
同理可得S△BQC=S△EFQ=25cm2，
∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2．
故答案为40．
点评：本题主要考查了平行四边形的性质，解答此题关键是作出辅助线，找出同底等高的三角形．
练习册系列答案
口算能手系列答案
相关题目
如图，△ABC为等腰直角三角形，∠C=90°，AC=6．动点O在△ABC的边上，从点A出发沿着A→C→B→A的路线匀速运动一周，速度为1个长度单位每秒，以O为圆心、半径为1的圆在运动过程中与△ABC的边BC相切时是出发后第
如图，直线y=-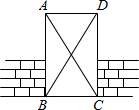
如图，工人师傅砌门时，要想检验门框ABCD是否符合设计要求（即门框是否为矩形），在确保两组对边分别平行的前提下，只要测量出对角线AC、BD的长度，然后看它们是否相等就可判断了．