题目内容
7．
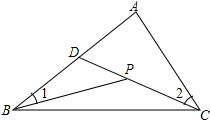如图，点P是△ABC内一点，CP的延长线交AB于D，连接BP．若∠1=25°，∠A=67°，∠2=40°，求∠BDC和∠BPC的度数．
分析 先根据三角形内角和定理求出∠ADC的度数，再由补角的定义得出∠BDC的度数，根据三角形外角的性质即可得出结论．
解答 解：在△ACD中，∵∠A=67°，∠2=40°，
∴∠ADC=180°-67°-40°=73°，
∴∠BDC=180°-73°=107°．
∵∠BPC是△BDP的外角，
∴∠BPC=∠1+∠BDC=25°+107°=132°．
点评 本题考查的是三角形外角的性质，熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键．
练习册系列答案
相关题目
17．
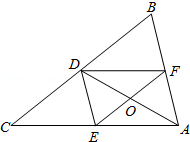如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．结论正确的是（ ）
如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．结论正确的是（ ）| A． | 0A=0D | B． | EF=DF | C． | AF=AE | D． | BD=DE |
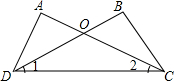题目：如图，已知AC，BD相交于点0．∠A=∠B，∠1=∠2，试说明△AOD≌△BOC．
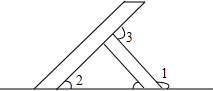一天，爸爸带小明到建筑工地玩，他们看到一个如图所示的人字架，爸爸说：“小明，我考考你，这个人字架的夹角∠1等于140°，你知道∠3比∠2大多少吗？”小明马上得到了正确的答案，他的答案是40°．
如图，在⊙O中，ON⊥CD，OM⊥AB，ON=3cm，OA=5cm，AB=8cm，求OM及CD的长．