题目内容
10.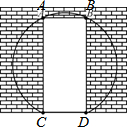 如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=$\frac{2}{3}\sqrt{3}$米.
如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=$\frac{2}{3}\sqrt{3}$米.(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
分析 (1)先证得BC是直径,在直角三角形BCD中,由BD与CD的长,利用勾股定理求出BC的长,即可求得半径;
(2)打掉墙体的面积=2(S扇形OAC-S△AOC)+S扇形OAB-S△AOB,根据扇形的面积和三角形的面积求出即可.
解答 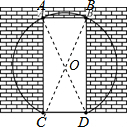 解:(1)连结AD、BC,
解:(1)连结AD、BC,
∵∠BDC=90°,
∴BC是直径,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\frac{4\sqrt{3}}{3}$
∴圆形门洞的半径为$\frac{2\sqrt{3}}{3}$.
(2)取圆心O,连结OA.由上题可知,OA=OB=AB=$\frac{2\sqrt{3}}{3}$,
∴△AOB是正三角形,
∴∠AOB=60°,∠AOC=120°,
∴S△AOB=$\frac{{\sqrt{3}}}{3}$,S△AOC=$\frac{{\sqrt{3}}}{3}$
∴S=2(S扇形OAC-S△AOC)+S扇形OAB-S△AOB
=2($\frac{120π×(\frac{2\sqrt{3}}{3})^{2}}{360}$-$\frac{\sqrt{3}}{3}$)+($\frac{60π×(\frac{2\sqrt{3}}{3})^{2}}{360}$-$\frac{\sqrt{3}}{3}$)
=$\frac{10}{9}$π-$\sqrt{3}$
∴打掉墙体面积为$\frac{10}{9}$π-$\sqrt{3}$平方米.
点评 本题考查了圆周角定理和垂径定理,扇形和三角形的面积,矩形的性质,关键是理解阴影部分的面积是由哪几部分图形组成的,然后利用公式求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
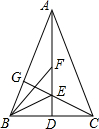 如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.
如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$. 如图,已知∠BAC=∠ACD,则可判断图中AB∥CD.
如图,已知∠BAC=∠ACD,则可判断图中AB∥CD.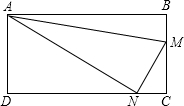 如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )
如图,在矩形ABCD中,AB=24,BC=12,M、N两点分别从点B、C开始沿边BC和CD匀速运动,如果点M、N同时出发,它们运动的速度均为每秒2个单位长度,当点M到达终点C时,点N也停止运动,设运动的时间为t(s).下列说法:①当t=3时,MN∥BD;②当t=6时,△AMN的面积最小;③当t=4时,S△ABM=S△AND;④不存在MN与AN垂直的时刻,正确的有( )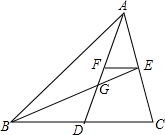 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.