题目内容
3．解方程组：$\left\{\begin{array}{l}{x-4y+2z=4}\\{2x-3y+2z=10}\\{3x-2y-z=4}\end{array}\right.$．分析 用加减消元法或代入消元法先把三元一次方程组化为二元一次方程组再求解．
解答 解：$\left\{\begin{array}{l}{x-4y+2z=4①}\\{2x-3y+2z=10②}\\{3x-2y-z=4③}\end{array}\right.$，
②-①得x+y=6④，
③×2+①得7x-8y=12⑤，
④与⑤组成方程组得$\left\{\begin{array}{l}{x+y=6}\\{7x-8y=12}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$，
代入①得z=4，
故原方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=2}\\{z=4}\end{array}\right.$．
点评 本题考查了解三元一次方程组，解三元一次方程组关键是先把三元一次方程组化为二元一次方程组，再用解二元一次方程组的知识求解．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
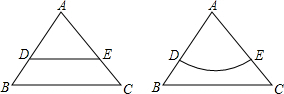如果是两个全等的等边三角形ABC，平行于BC的线段DE与以点A为圆心的$\widehat{DE}$把△ABC的面积分成相等的两部分，则线段DE的长小于$\widehat{DE}$的长．（填“大于”“小于”或“等于”）