题目内容
12.如图,在长方形纸带中,∠DEF=20°,将纸带沿EF折叠后,再沿BF折叠.那么折叠后的图形中∠CFE的度数是120°.
分析 在图b中由翻折的性质可知:∠D′EF=∠FEG=20°,然后根据平行线的性质可知∠BGE=∠D′EG=40°,∠GFE=∠D′EF=20°,在图C中,∠FGD′=∠EGB=40°,由翻折的性质可知:∠DGF=∠D′GF=40°,由三角形的外角的性质可知∠DHF=∠DGF+∠HFG=60°,然后由平行线的性质可求得:∠CFE=180°-∠DHF=120°.
解答 解:如图所示:
在图b中由翻折的性质可知:∠D′EF=∠FEG=20°,
∵ED′∥GF,
∴∠BGE=∠D′EG=40°,∠GFE=∠D′EF=20°.
在图C中,∠FGD′=∠EGB=40°,
由翻折的性质可知:∠DGF=∠D′GF=40°.
∠DHF=∠DGF+∠HFG=40°+20°=60°.
∵HD∥FC,
∴∠DHF+∠CFE=180°.
∴∠CFE=180°-∠DHF=180°-60°=120°.
故答案为:120.
点评 本题主要考查的是翻折的性质,根据翻折的性质和平行线的性质进行角的转化是解题的关键.

练习册系列答案
相关题目
 如图,已知BD=AC,那么添加一个BC=AD条件后,能得到△ABC≌△BAD(只填一个即可).
如图,已知BD=AC,那么添加一个BC=AD条件后,能得到△ABC≌△BAD(只填一个即可). 汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性,如图,三个汉字可以看成是轴对称图形.
汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性,如图,三个汉字可以看成是轴对称图形.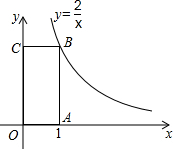 如图,点B在反比例函数y=$\frac{2}{x}$(x>0)的图象上,过B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )
如图,点B在反比例函数y=$\frac{2}{x}$(x>0)的图象上,过B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )