题目内容
已知α,β是方程x2-6x-5=0的两个根,求α2+6β+13的值.
考点:根与系数的关系,一元二次方程的解
专题:计算题
分析:先根据一元二次方程的解的定义得到α2-6α-5=0,即α2=6α+5,则α2+6β+13可化简为6(α+β)+18,再根据根与系数的关系得到α+β=6,然后利用整体代入的方法计算.
解答:解:∵α是方程x2-6x-5=0的根,
∴α2-6α-5=0,即α2=6α+5,
∴α2+6β+13=6α+5+6β+13
=6(α+β)+18,
∵α,β是方程x2-6x-5=0的两个根,
∴α+β=6,
∴α2+6β+13=6×6+18=54.
∴α2-6α-5=0,即α2=6α+5,
∴α2+6β+13=6α+5+6β+13
=6(α+β)+18,
∵α,β是方程x2-6x-5=0的两个根,
∴α+β=6,
∴α2+6β+13=6×6+18=54.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了一元二次方程的解.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
关于x的方程
+3=
有增根,则m的值为( )
| 7 |
| x-1 |
| m |
| x-1 |
| A、x=1 | B、x=-1 |
| C、x=7 | D、x=-7 |
如图所示的图案中不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
某商店先进货7辆自行车,平均每辆自行车a元,后来又进货5辆自行车,平均每辆自行车b元,后来商店以每辆
的价格把自行车全部卖掉了,结果发现赔了钱,赔钱的原因是( )
| a+b |
| 2 |
| A、a=b | B、a<b |
| C、与a、b的大小无关 | D、a>b |
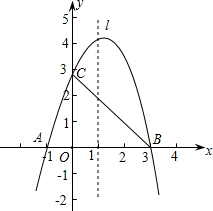 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴,
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴,