题目内容
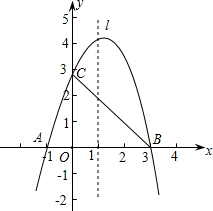 已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴,
已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴,(1)求抛物线的函数解析式;
(2)在y轴上有一个点D,使△AOD和△BOC相似,求点D坐标.
考点:二次函数综合题
专题:
分析:(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可.
(2)根据题意可知△BOC为等腰直角三角形,然后找出与点D,使△AOD和△BOC相似.
(2)根据题意可知△BOC为等腰直角三角形,然后找出与点D,使△AOD和△BOC相似.
解答:解:(1)将点A(-1,0),B(3,0),C(0,3)代入抛物线y=ax2+bx+c得,
,
解得:
.
则抛物线解析式为:y=-x2+2x+3;
(2)由题意得,△BOC为等腰直角三角形,
要使△AOD和△BOC相似,
则
=
,
代入得:
=
,
解得:OD=1,
则点D的坐标为(0,1)或(0,-1).
|
解得:
|
则抛物线解析式为:y=-x2+2x+3;
(2)由题意得,△BOC为等腰直角三角形,
要使△AOD和△BOC相似,
则
| OD |
| AO |
| CO |
| BO |
代入得:
| OD |
| 1 |
| 3 |
| 3 |
解得:OD=1,
则点D的坐标为(0,1)或(0,-1).
点评:本题考查了二次函数的综合应用,涉及了抛物线的性质、待定系数法求解析式、等腰直角三角形的判定、相似三角形的性质等知识,解题的关键是注意点D有两个位置,一个在y轴正半轴一个在y轴负半轴,注意不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
填空:
(1)绝对值是7的数是 ;
(2)绝对值小于3.9的整数 ;
(3)当a>0时,|2a|= ;
(4)当a>1时,|a-1|= ;
(5)当a<1时,|a-1|= ?
(6)如果a>3,则|3-a|= .
(1)绝对值是7的数是
(2)绝对值小于3.9的整数
(3)当a>0时,|2a|=
(4)当a>1时,|a-1|=
(5)当a<1时,|a-1|=
(6)如果a>3,则|3-a|=