题目内容
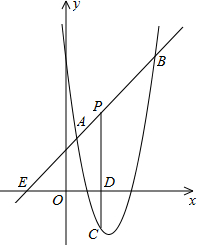 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(| 1 |
| 2 |
| 5 |
| 2 |
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
考点:二次函数综合题
专题:几何综合题,压轴题
分析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.
(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.
(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.
(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
解答:解:(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A(
,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴
,解得
,
∴抛物线的解析式为y=2x2-8x+6.
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6),
=-2n2+9n-4,
=-2(n-
)2+
,
∵PC>0,
∴当n=
时,线段PC最大且为
.
(3)∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3-1,过点A(
,
)作AN⊥x轴于点N,则ON=
,AN=
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=
,∴OM=ON+MN=
+
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则:
,解得
,
∴直线AM的解析式为:y=-x+3 ①
又抛物线的解析式为:y=2x2-8x+6 ②
联立①②式,解得:x=3或x=
(与点A重合,舍去)
∴C(3,0),即点C、M、D重合.
当x=3时,y=x+2=5,
∴P1(3,5);
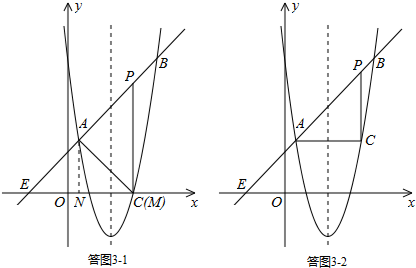
iii)若点C为直角顶点,则∠ACP=90°.
∵y=2x2-8x+6=2(x-2)2-2,
∴抛物线的对称轴为直线x=2.
如答图3-2,作点A(
,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C(
,
).
当x=
时,y=x+2=
.
∴P2(
,
).
∵点P1(3,5)、P2(
,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(
,
).
∴m=4+2=6,
∴B(4,6),
∵A(
| 1 |
| 2 |
| 5 |
| 2 |
∴
|
|
∴抛物线的解析式为y=2x2-8x+6.
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6),
=-2n2+9n-4,
=-2(n-
| 9 |
| 4 |
| 49 |
| 8 |
∵PC>0,
∴当n=
| 9 |
| 4 |
| 49 |
| 8 |
(3)∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3-1,过点A(
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则:
|
|
∴直线AM的解析式为:y=-x+3 ①
又抛物线的解析式为:y=2x2-8x+6 ②
联立①②式,解得:x=3或x=
| 1 |
| 2 |
∴C(3,0),即点C、M、D重合.
当x=3时,y=x+2=5,
∴P1(3,5);

iii)若点C为直角顶点,则∠ACP=90°.
∵y=2x2-8x+6=2(x-2)2-2,
∴抛物线的对称轴为直线x=2.
如答图3-2,作点A(
| 1 |
| 2 |
| 5 |
| 2 |
则点C在抛物线上,且C(
| 7 |
| 2 |
| 5 |
| 2 |
当x=
| 7 |
| 2 |
| 11 |
| 2 |
∴P2(
| 7 |
| 2 |
| 11 |
| 2 |
∵点P1(3,5)、P2(
| 7 |
| 2 |
| 11 |
| 2 |
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(
| 7 |
| 2 |
| 11 |
| 2 |
点评:此题主要考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )
如图,数轴上有A、B、C、D四个点,其中表示互为相反数的点是( )| A、点A与点D |
| B、点A与点C |
| C、点B与点D |
| D、点B与点C |
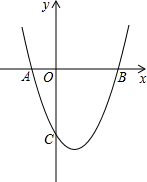 如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
如图,抛物线y=x2+mx+(m-1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.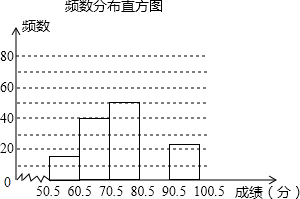 某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)作样本进行统计分析,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)作样本进行统计分析,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题: