题目内容
在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点O,若AC=7,则线段AO的长度等于 .
考点:平行四边形的判定与性质
专题:
分析:根据在四边形ABCD中,AB∥CD,AD∥BC,得出四边形ABCD是平行四边形,然后即可求解.
解答: 解:∵在四边形ABCD中,AB∥CD,AD∥BC,
解:∵在四边形ABCD中,AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵AC=7,
∴AO=
AC=
×7=
.
故答案为:
.
 解:∵在四边形ABCD中,AB∥CD,AD∥BC,
解:∵在四边形ABCD中,AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,
∵AC=7,
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:此题主要考查了平行四边形的判定与性质,得出四边形ABCD是平行四边形是解题关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
用一副三角板(两块)画角,画出的角的度数不可能是( )
| A、135° | B、75° |
| C、55° | D、15° |
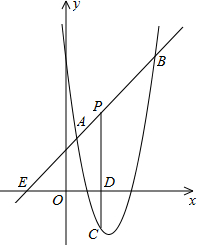 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( 如图,数轴上A、B两点之间的距离为
如图,数轴上A、B两点之间的距离为 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值=
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值=