题目内容
8. 如图,在△ABC中,D是BC上一点,且AB=BD=3CD,若cos∠DAC=$\frac{7}{8}$,AD=6,则AC=8.
如图,在△ABC中,D是BC上一点,且AB=BD=3CD,若cos∠DAC=$\frac{7}{8}$,AD=6,则AC=8.
分析 作CE⊥AD,BF⊥AD垂足分别为E、F,由△BFD∽△CED得$\frac{BF}{CE}=\frac{BD}{CD}$=$\frac{DF}{DE}$=3,因为AF=FD=3,可以求出DE=1,AE=7,再在RT△AEC利用cos∠EAC求出AC即可.
解答 解:作CE⊥AD,BF⊥AD垂足分别为E、F.
∵∠BFE=∠CEA=90°,
∴BF∥CE,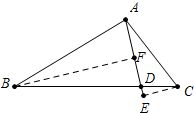
∴△BFD∽△CED,
∴$\frac{BF}{CE}=\frac{BD}{CD}$=$\frac{DF}{DE}$=3,
∵BA=BD,BF⊥AD,
∴AF=DF=3,DE=1,
在RT△AEC中,∵∠AEC=90°,AE=7,cos∠EAC=$\frac{7}{8}$,
∴$\frac{AE}{AC}=\frac{7}{8}$,
∴AC=8.
故答案为8.
点评 本题考查相似三角形的性质、三角函数等知识,解题的关键是由三角形相似得出边的比例关系,求出相应的线段,记住等腰三角形的高是常用辅助线.

练习册系列答案
相关题目
18.某青年排球队10名队员的年龄如下:20,20,18,19,19,19,21,21,22,22,该队队员年龄的众数与中位数分别是( )
| A. | 20岁,19岁 | B. | 19岁,19岁 | C. | 19岁,20.5岁 | D. | 19岁,20岁 |
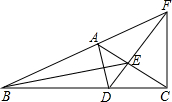 如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.



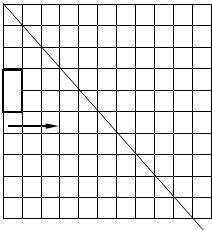 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线 ”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
 表示的自然数是18;
表示的自然数是18; .
.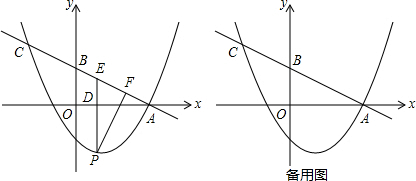
 如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.
如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.