题目内容
在△ABC中，∠A-∠B=20°，∠B-∠C=20°，那么∠A= ，∠C= ．
考点：三角形内角和定理
专题：
分析：设∠B=x，则∠A=20°+x，∠C=x-20°，根据三角形的内角和定理列出方程求出x的值，进而可得出结论．
解答：解：∵在△ABC中，∠A-∠B=20°，∠B-∠C=20°，
∴设∠B=x，则∠A=20°+x，∠C=x-20°，
∵∠A+∠B+∠C=180°，即（20°+x）+x+（x-20°）=180°，解得x=60°，
∴∠A=x+20=60°+20°=80°，∠C=x-20°=60°-20°=40°．
故答案为：80°，40°．
∴设∠B=x，则∠A=20°+x，∠C=x-20°，
∵∠A+∠B+∠C=180°，即（20°+x）+x+（x-20°）=180°，解得x=60°，
∴∠A=x+20=60°+20°=80°，∠C=x-20°=60°-20°=40°．
故答案为：80°，40°．
点评：本题考查了三角形的内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
相关题目
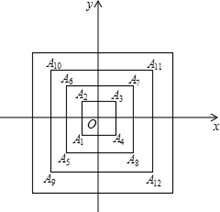如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A2014的坐标是
如图，AC是⊙O的弦，以OA为直径的圆交AC于点E．
如果一个多边形的每一个外角都是45°，那么这个多边形的内角和是（ ）
| A、540° | B、720° |
| C、1080° | D、1260° |
△ABC中，∠A=60°，∠ABC和∠ACB的平分线相交于点P，则∠BPC=