题目内容
 △ABC中,∠A=60°,∠ABC和∠ACB的平分线相交于点P,则∠BPC=
△ABC中,∠A=60°,∠ABC和∠ACB的平分线相交于点P,则∠BPC=考点:三角形内角和定理
专题:
分析:根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.
解答:解:∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=
×120°=60°,
在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=180°-60°=120°.
故答案为:120°.
∴∠ABC+∠ACB=180°-60°=120°,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=180°-60°=120°.
故答案为:120°.
点评:本题考查了三角形的内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下列一元二次方程最适合用分解因式法来解的是( )
| A、(x+1)(x-3)=2 |
| B、2(x-2)2=x2-4 |
| C、x2+3x-1=0 |
| D、5(2-x)2=3 |
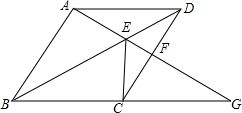 四边形ABCD是边长为2的菱形,点G是BC延长线上一点,连接AG,AG⊥AB,分别交DB、CD于点E、F,连接CE.若AE=2EF,求EF长.
四边形ABCD是边长为2的菱形,点G是BC延长线上一点,连接AG,AG⊥AB,分别交DB、CD于点E、F,连接CE.若AE=2EF,求EF长. 如图,⊙O的弦AB垂直平分半径OC,若AB=2,则⊙O的半径为
如图,⊙O的弦AB垂直平分半径OC,若AB=2,则⊙O的半径为