题目内容
已知a、b满足条件(a2+b2)(a2+b2+1)=12,则a2+b2的值为 .
考点:换元法解一元二次方程
专题:
分析:设t=a2+b2,则原方程转化为t(t+1)=12,通过解该方程求得的值,即a2+b2的值.
解答:解:设t=a2+b2,则原方程转化为t(t+1)=12,
整理,得
(t+4)(t-3)=0,
解得 t1=-4(舍去),t2=3,
则t=a2+b2=3.
故答案是:3.
整理,得
(t+4)(t-3)=0,
解得 t1=-4(舍去),t2=3,
则t=a2+b2=3.
故答案是:3.
点评:本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
相关题目
已知点M(1,a)和点N(2,b)是一次函数y=(k-2)x-3图象上的两点,若a>b,则k的取值范围是( )
| A、k>2 | B、k<0 |
| C、k<2 | D、k≤2 |
数据1、2、5、3、5、3、5的众数是( )
| A、1 | B、2 | C、3 | D、5 |
 如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么? 如图,在△ABC中,AB=AC=10,BC=12,AH⊥BC于H,点P从点B出发沿射线BC以每秒3个单位长度的速度运动,点Q从点C出发沿CA边以每秒2个单位长度的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交AH所在直线于点E.若P、Q两点同时出发,当点Q运动到点A时,P、Q两点停止运动,设运动时间为t秒(t>0).
如图,在△ABC中,AB=AC=10,BC=12,AH⊥BC于H,点P从点B出发沿射线BC以每秒3个单位长度的速度运动,点Q从点C出发沿CA边以每秒2个单位长度的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交AH所在直线于点E.若P、Q两点同时出发,当点Q运动到点A时,P、Q两点停止运动,设运动时间为t秒(t>0).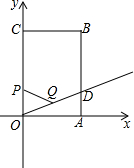 已知如图,矩形OABC在平面直角坐标系中,OA=
已知如图,矩形OABC在平面直角坐标系中,OA=