题目内容
如图，在⊙O的内接四边形ABCD中，DB=DC，∠DAE是四边形ABCD的一个外角．∠DAE与∠DAC相等吗？为什么？考点：圆内接四边形的性质,等腰三角形的性质,圆周角定理
专题：
分析：首先利用等腰三角形的性质得出∠DBC=∠DCB，进而利用圆内接四边形的性质得出∠EAD=∠DCB，再利用圆周角定理求出∠DAE与∠DAC相等．
解答：解：∠DAE与∠DAC相等，
理由：∵DB=DC，
∠DBC=∠DCB，
∵∠DAE是四边形ABCD的一个外角，
∴∠EAD=∠DCB，
∴∠DBC=∠EAD，
又∵∠DAC=∠DBC，
∴∠DAE=∠DAC．
理由：∵DB=DC，
∠DBC=∠DCB，
∵∠DAE是四边形ABCD的一个外角，
∴∠EAD=∠DCB，
∴∠DBC=∠EAD，
又∵∠DAC=∠DBC，
∴∠DAE=∠DAC．
点评：此题主要考查了等腰三角形的性质、圆内接四边形的性质、圆周角定理等知识，得出∠DBC=∠EAD是解题关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知二次函数y=2x2
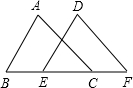如图，已知：在△ABC和△DEF中，如果AB=DE，BC=EF．在下列条件中不能保证△ABC≌△DEF的是（ ）| A、∠B=∠DEF |
| B、AC=DF |
| C、AB∥DE |
| D、∠A=∠D |