题目内容
10.在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,D是垂足,如果BD=3cm,那么AB=12cm.分析 先由三角形内角和定理可得:∠B=60°,然后由CD⊥AB,可得:∠BDC=90°,进而可得∠BCD=30°,然后根据30°角所对的直角边等于斜边的一半,可得BC=2BD=6,然后再根据30°角所对的直角边等于斜边的一半,可得:AB=2BC=12.
解答 解:如图所示,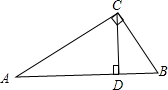
∵△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,又CD⊥AB,
∴∠BCD=30°,
在Rt△BCD中,∠BCD=30°,BD=3cm,
可得BC=2BD=6cm,
在Rt△ABC中,∠A=30°,BC=6cm,
则AB=2BC=12cm.
故答案为:12.
点评 此题考查了含30°角直角三角形的性质,以及三角形的内角和定理,熟练掌握性质是解本题的关键.

练习册系列答案
相关题目
2.满足(2-m)m2-m-2=1的所有实数m的和为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
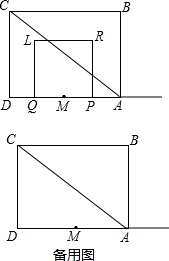 如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.
如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.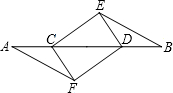 如图,已知AF∥BE,且AF=BE,AC=BD.请指出图中有哪些全等三角形,并任选一对给予证明.
如图,已知AF∥BE,且AF=BE,AC=BD.请指出图中有哪些全等三角形,并任选一对给予证明.