题目内容
20.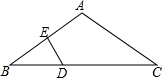 已知:如图,在△ABC中,AB=AC,∠BAC=120°,DE⊥AB,且BE=AE.求证:DC=2BD.
已知:如图,在△ABC中,AB=AC,∠BAC=120°,DE⊥AB,且BE=AE.求证:DC=2BD.
分析 连结AD.在△ABC中,根据等边对等角的性质及三角形内角和定理求出∠B=∠C=$\frac{1}{2}$(180°-∠BAC)=30°.由DE是AB的垂直平分线得出AD=BD,那么∠BAD=∠B=30°,那么∠DAC=∠BAC-∠BAD=90°.然后在Rt△ADC中,根据30°角所对的直角边等于斜边的一半,得出DC=2AD,等量代换即可得到DC=2BD.
解答 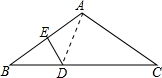 证明:连结AD.
证明:连结AD.
∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac{1}{2}$(180°-∠BAC)=30°.
∵DE⊥AB,BE=AE,
∴AD=BD,
∴∠BAD=∠B=30°,
∴∠DAC=∠BAC-∠BAD=120°-30°=90°.
∵在Rt△ADC中,∠DAC=90°,∠C=30°,
∴DC=2AD,
∴DC=2BD.
点评 本题考查了含30度角的直角三角形的性质,等腰三角形的性质,三角形内角和定理,垂直平分线的性质,难度适中,熟记性质是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 整数和分数统称为有理数 | |
| B. | 最小的有理数是0 | |
| C. | 正整数、负整数、正分数、负分数统称为有理数 | |
| D. | 0不是有理数 |
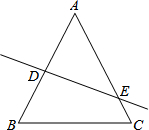 如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.
如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.