题目内容
19. 已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.
已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.
分析 求出两个正方形的边长,根据面积大的比较合理来选择.
解答 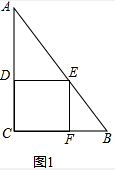 解:图1中,设DE=CD=EF=CF=x,
解:图1中,设DE=CD=EF=CF=x,
∵DE∥BC,
∴$\frac{DE}{BC}=\frac{AD}{AC}$,
∴$\frac{x}{6}=\frac{8-x}{8}$,
∴x=$\frac{24}{7}$,
图2中,作CM⊥AB垂足为M交DE于N.设正方形DEFG边长为y.
在RT△ABC中,∵AC=8,BC=6,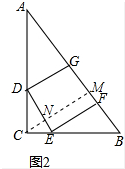 ∴AB=$\sqrt{C{A}^{2}+B{C}^{2}}$=10,CM=$\frac{AC•BC}{AB}$=4.8,
∴AB=$\sqrt{C{A}^{2}+B{C}^{2}}$=10,CM=$\frac{AC•BC}{AB}$=4.8,
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{DE}{AB}=\frac{CN}{CM}$,
∴$\frac{y}{10}=\frac{4.8-y}{4.8}$,
∴y=$\frac{120}{37}$.
∵x>y,
∴图1中正方形面积大,
故图1的剪法较为合理.
点评 本题考查相似三角形的应用、平行线分线段成比例定理、正方形的面积等知识,解题的关键是根据相似三角形的性质列出方程解决问题,学会转化的思想思考问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.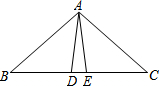 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )| A. | △ABE≌△ACD | B. | △ABD≌△ACE | C. | ∠C=30° | D. | ∠DAE=40° |
4.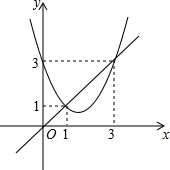 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2-4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b-1)x+c<0.
其中正确的个数为( )
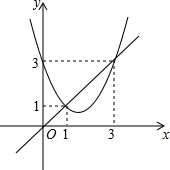 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b-1)x+c<0.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.某单位有1000名员工,从中随机抽取100名员工进行年薪的调查,下列说法中正确的是( )
| A. | 这种抽查方式是普查 | B. | 1000名员工是总体 | ||
| C. | 每名员工的年薪是个体 | D. | 100名员工是总体的一个样本 |
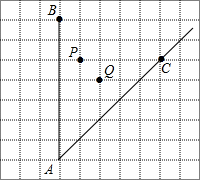 如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.
如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小. 如图,已知AE=AC,AD=AB,∠1=∠2,求证:△EAD≌△CAB.
如图,已知AE=AC,AD=AB,∠1=∠2,求证:△EAD≌△CAB.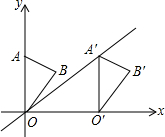 如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△0′A′B′,A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△0′A′B′,A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为( )