题目内容
18.关于x的方程x2-(2k+1)x+k2=0,当k取何值时,此方程:(1)有两个不等实数根;
(2)有两个相等的实数根;
(3)没有实数根;
(4)有一根为1.
分析 (1)(2)(3)根据一元二次方程根的情况与判别式△的关系确定k的取值;
(4)把根代入方程求得k的数值即可.
解答 解:∵a=1,b=-(2k+1),c=k2,
∴△=b2-4ac=[-(2k+1)]2-4×1×k2=4k+1,
(1)∵方程有两个不相等的实数根,
∴△>0,
即4k+1>0,
解得k>-$\frac{1}{4}$.
(2)∵方程有两个相等的实数根,
∴△=0,
即4k+1=0,
解得k=-$\frac{1}{4}$.
(3)∵方程没有实数根,
∴△<0,
即4k+1<0,
解得k<-$\frac{1}{4}$.
(4)∵有一根为1,
∴k2-2k=0,
解得k=1或k=0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.若y=ax2+bx+c,则由表中信息可知:y与x之间的函数关系式是( )
| x | -1 | 0 | 1 |
| ax2 | |||
| ax2+bx+c | 8 | 3 | 0 |
| A. | y=x2-4x+3 | B. | y=x2-2x+4 | C. | y=x2-3x+3 | D. | y=x2-4x+8 |
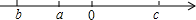 已知a,b,c在数轴上的位置如图所示,确定下列各式与0的大小关系.
已知a,b,c在数轴上的位置如图所示,确定下列各式与0的大小关系.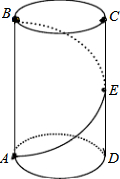 如图,一只螳螂在树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是就绕到虫子后面吃掉它,已知树干的半径为10cm,A,B两点的距离为45cm,求螳螂爬行的最短距离(π取3).
如图,一只螳螂在树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是就绕到虫子后面吃掉它,已知树干的半径为10cm,A,B两点的距离为45cm,求螳螂爬行的最短距离(π取3).