题目内容
3.先化简,再求值:-(-2a)3•(-b3)2+(-$\frac{3}{2}$ab2)3,其中a=-$\frac{1}{2}$,b=2.分析 先算乘方和乘法,再合并同类项,最后代入求出即可.
解答 解:-(-2a)3•(-b3)2+(-$\frac{3}{2}$ab2)3,
=8a3b6+(-$\frac{27}{8}$a3b6)
=$\frac{37}{8}$a3b6,
其当a=-$\frac{1}{2}$,b=2时,原式=-37.
点评 本题考查了整式的混合运算和求值的应用,能正确根据整式的运算法则进行化简是解此题的关键,

练习册系列答案
相关题目
14.如图,在平面直角坐标系中,用描点法分别画出函数y=-x+1与y=-$\frac{2}{x}$的图象,并写出不等式-x+1>-$\frac{2}{x}$的解集.
解:列表:
画图象:
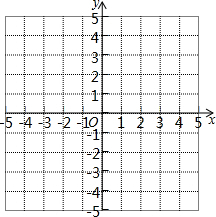
不等式-x+1>-$\frac{2}{x}$的解集为x<-1或0<x<2.
解:列表:
| x | … | … | ||||||
| y=-x+1 | … | … | ||||||
| y=-$\frac{2}{x}$ | … | … |

不等式-x+1>-$\frac{2}{x}$的解集为x<-1或0<x<2.
11.化简$\sqrt{(m-5)^{2}(5-m)}$的正确结果是( )
| A. | (m-5)$\sqrt{5-m}$ | B. | (5-m)$\sqrt{5-m}$ | C. | m-5$\sqrt{-(5-m)}$ | D. | 5-m$\sqrt{5-m}$ |
18.在实数范围内,$\sqrt{x+1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≥-1 | C. | x≤1 | D. | x≤-1 |
8.若1<x<2,则$\sqrt{4-4x+{x}^{2}}$+$\sqrt{{x}^{2}+2x+1}$化简的结果是( )
| A. | 2x-1 | B. | -2x+1 | C. | -3 | D. | 3 |
11.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°,则∠NPB的度数是( )
| A. | 50° | B. | 60° | C. | 40°或140° | D. | 50°或130° |
 中,
中,  .点
.点 从点
从点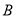 出发沿线段
出发沿线段 移动,同时点
移动,同时点 从点
从点 出发沿线段
出发沿线段 的延长线移动,点
的延长线移动,点 、
、 移动的速度相同,
移动的速度相同,  与直线
与直线 相交于点
相交于点 .
. 为
为 的中点时,求
的中点时,求 的长;
的长; 作直线
作直线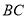 的垂线,垂足为
的垂线,垂足为 ,当点
,当点 、
、 在移动的过程中,设
在移动的过程中,设 ,
,  是否为常数?若是请求出
是否为常数?若是请求出 的值,若不是请说明理由.
的值,若不是请说明理由.


