题目内容
5. 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取4$\sqrt{3}$=7)
(3)运动员乙要抢到足球第二个落点D,他应再向前跑多少米?(取2$\sqrt{6}$=5)
分析 (1)依题意设抛物线顶点式,将点A坐标代入可得抛物线的表达式.
(2)令y=0可求出x的两个值,再按实际情况筛选.
(3)如图可得第二次足球弹出后的距离为CD,依题意可知CD=EF,从而得方程-$\frac{1}{12}$(x-6)2+4=2解得x的值即可知道CD、BD.
解答 解:(1)根据题意,可设第一次落地时,抛物线的表达式为y=a(x-6)2+4,
将点A(0,1)代入,得:36a+4=1,
解得:a=-$\frac{1}{12}$,
∴足球开始飞出到第一次落地时,该抛物线的表达式为y=-$\frac{1}{12}$(x-6)2+4;
(2)令y=0,得:-$\frac{1}{12}$(x-6)2+4=0,
解得:x1=4$\sqrt{3}$+6≈13,x2=-4$\sqrt{3}$+6<0(舍去),
∴足球第一次落地点C距守门员13米;
(3)如图,足球第二次弹出后的距离为CD,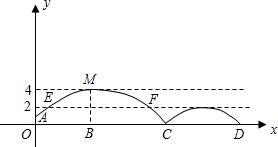
根据题意知CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),
∴-$\frac{1}{12}$(x-6)2+4=2,
解得:x1=6-2$\sqrt{6}$,x2=6+2$\sqrt{6}$,
∴CD=x2-x1=4$\sqrt{6}$≈10,
∴BD=13-6+10=17米,
答:运动员乙要抢到足球第二个落点D,他应再向前跑17米.
点评 本题主要考查二次函数应用问题,解题的关键是要有建模思想,将题目中的语句转化为数学语言,这样才能较好的领会题意并运用自己的知识解决问题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
20.某校抽取10名学生参加“心理健康”知识测试,他们得分情况如表:
那么这10名学生所得分数的众数和中位数分别是( )
| 分数 | 80 | 85 | 90 | 85 |
| 人数 | 2 | 3 | 4 | 1 |
| A. | 95和85 | B. | 90和85 | C. | 90和87.5 | D. | 85和87.5 |
17.已知am=2,an=$\frac{1}{2}$,a2m+3n的值为( )
| A. | 6 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{11}{2}$ |
15.200粒大米重约4克,如果每人每天浪费1粒米,那么约458万人口的漳州市每天浪费大米用科学记数法表示约为( )
| A. | 9.16×103克 | B. | 9.16×104克 | C. | 9,16×105克 | D. | 0.916×105克 |
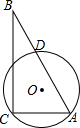 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.
如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.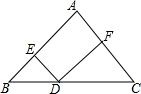 如图,在△ABC中,AB=AC=8,D是BC上一动点(D与B、C不重合),且DE∥AC,DF∥AB,则四边形DEAF的周长是16.
如图,在△ABC中,AB=AC=8,D是BC上一动点(D与B、C不重合),且DE∥AC,DF∥AB,则四边形DEAF的周长是16.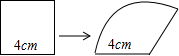 手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.
手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.