题目内容
已知x3+x2+x+1=0,则x2004+x2003+x2002+…+x2+x+1= .
考点:因式分解的应用
专题:
分析:观察整式x+x2+x3+…+x2004通过提取公因式,可分解为含有因式1+x+x2+x3的形式.再将1+x+x2+x3的值作为一个整体代入求解.
解答:解:∵1+x+x2+x3=0,
∴1+x+x2+x3+…+x2004
=1+x(1+x+x2+x3)+x5(1+x+x2+x3)+x9(1+x+x2+x3)+…+x1997(1+x+x2+x3)+x2001(1+x+x2+x3)
=1+(1+x+x2+x3)(x+x5+x9+x12+…+x1997+x2001)
=1+0
=1.
故答案为:1.
∴1+x+x2+x3+…+x2004
=1+x(1+x+x2+x3)+x5(1+x+x2+x3)+x9(1+x+x2+x3)+…+x1997(1+x+x2+x3)+x2001(1+x+x2+x3)
=1+(1+x+x2+x3)(x+x5+x9+x12+…+x1997+x2001)
=1+0
=1.
故答案为:1.
点评:本题考查了因式分解的运用,解决本题的关键是对x+x2+x3+…+x2004分解成为含有因式1+x+x2+x3的形式.

练习册系列答案
相关题目
若(x+k)(x-5)的积中不含有x的一次项,则k的值是( )
| A、0 | B、5 | C、-5 | D、-5或5 |
将二次函数y=x2-2x+3化为y=(x+m)2+h的形式,结果为( )
| A、y=(x-1)2+4 |
| B、y=(x+1)2+4 |
| C、y=(x-1)2+2 |
| D、y=(x+1)2+2 |




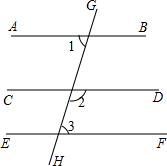 如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 )
如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 )