题目内容
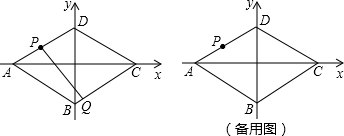
 如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.(1)求OC的长;
(2)求四边形OBEC的面积.
考点:菱形的性质
专题:
分析:(1)在直角△OCD中,利用勾股定理即可求解;
(2)利用矩形的定义即可证明,再利用矩形的面积公式即可直接求解.
(2)利用矩形的定义即可证明,再利用矩形的面积公式即可直接求解.
解答:解:(1)∵ABCD是菱形,
∴AC⊥BD,
∴直角△OCD中,OC=
=
=4(cm);
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形,
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形,
∵OB=0D,
∴S矩形OBEC=OB•OC=4×3=12(cm2).
∴AC⊥BD,
∴直角△OCD中,OC=
| CD2-OD2 |
| 52-32 |
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形,
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形,
∵OB=0D,
∴S矩形OBEC=OB•OC=4×3=12(cm2).
点评:本题考查了菱形的性质以及矩形的判定,理解菱形的对角线的关系是关键.

练习册系列答案
相关题目
将二次函数y=2x2-8x-1化成y=a(x-h)2+k的形式,结果为( )
| A、y=2(x-2)2-1 |
| B、y=2(x-4)2+32 |
| C、y=2(x-2)2-9 |
| D、y=2(x-4)2-33 |