题目内容
18.解方程组:(1)$\left\{\begin{array}{l}3x-5y=3\\ \frac{x}{2}-\frac{y}{3}=1\end{array}\right.$
(2)$\left\{\begin{array}{l}x+y-z=11\\ y+z-x=5\\ z+x-y=1\end{array}\right.$.
分析 (1)先把②去掉分母,再①-③求出y的值,然后代入①求出x的值,从而得出方程组的解;
(2)先①+②求出y的值,再③-②得出x-y=-2,求出x的值,然后把x、y的值代入①求出z的值,即可得出方程组的解.
解答 解:(1)$\left\{\begin{array}{l}{3x-5y=3①}\\{\frac{x}{2}-\frac{y}{3}=1②}\end{array}\right.$,
由②得:3x-2y=6③,
①-③得:-3y=-3,
解得:y=1,
把y=1代入①得:x=$\frac{8}{3}$,
则原方程组的解是:$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=1}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{x+y-z=11①}\\{y+z-x=5②}\\{z+x-y=1③}\end{array}\right.$,
①+②得:y=8④,
③-②得:x-y=-2⑤,
④+⑤得:x=6,
把x=6,y=8代入①得:z=3,
则原方程组的解为:$\left\{\begin{array}{l}{x=6}\\{y=8}\\{z=3}\end{array}\right.$.
点评 本题考查了解二元一次方程组和三元一次方程组,解三元一次方程组先转化为二元一次方程组,求出二元一次方程组的解,再求出第三个未知数的值.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
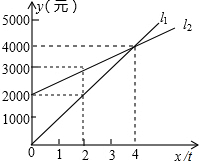 L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:
L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空: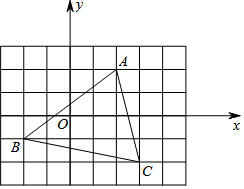 如图,△ABC在平面直角坐标系中:
如图,△ABC在平面直角坐标系中: