题目内容
18．设x1，x2是一元二次方程6x2+12x-9=0的两个实数根，不解方程，求下列各式的值．（1）|x1-x2|
（2）x13+x23．
分析 （1）先根据一元二次方程根与系数的关系确定出x1与x2的两根之积与两根之和的值，代入所求的代数式即可得到结果；
（2）先根据一元二次方程根与系数的关系确定出x1与x2的两根之积与两根之和的值，代入所求的代数式即可得到结果；
解答 解：根据题意得：x1+x2=-$\frac{12}{6}$=-2，x1•x2=$\frac{-9}{6}$=-$\frac{3}{2}$，
（1）|x1-x2|=$\sqrt{{{（x}_{1}{-x}_{2}）}^{2}}$=$\sqrt{{{（x}_{1}{+x}_{2}）}^{2}-{4x}_{1}{•x}_{2}}$=$\sqrt{{（-2）}^{2}-4×（-\frac{3}{2}）}$=$\sqrt{10}$，
（2）x13+x23．=（x1+x2）[${{（x}_{1}{+x}_{2}）}^{2}$-3x1•x2]=-17．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-$\frac{b}{a}$x1•x2=$\frac{c}{a}$．也考查了代数式的变形能力．
练习册系列答案
相关题目
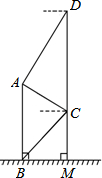在数学活动课上，为测量教学楼前的一座雕塑AB的高度．小明在二楼C处，利用测角仪测得雕塑顶端A处的仰角为30°，底部B处的俯角为45°，小华在五楼D处，利用测角仪测得雕塑顶端A处的俯角为60°．若CD为10米，请求出雕塑AB的高度．（结果精确到0.1米，参考数据$\sqrt{3}$≈1.73，$\sqrt{2}$≈1.41）．
6．取1张红桃，2张黑桃扑克牌，洗匀后，从这3张牌中任取1张牌恰好是黑桃的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | 1 |
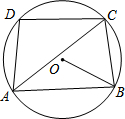如图，四边形ABCD为⊙O的内接四边形，连接AC、BO，已知∠CAB=36°，∠ABO=30°，则∠D=96°．