题目内容
3. 如图.?ABCD中,E为AB中点,G为AC上一点,AG:GC=1:4,连接EC并延长交AD于点F.求$\frac{DF}{FA}$的值.
如图.?ABCD中,E为AB中点,G为AC上一点,AG:GC=1:4,连接EC并延长交AD于点F.求$\frac{DF}{FA}$的值.
分析 连接BD、OE,根据四边形ABCD是平行四边形得出OA=OC,再根据AG:GC=1:4,证出AG:OG=2:5,再利用E是AC的中点,得出AF:OE=AG:OG=2:5,最后根据AD:AF=5:1,即可得出$\frac{DF}{FA}$=4.
解答 解:连接BD、OE,
∵四边形ABCD是平行四边形,
∴OA=OC,
∵AG:GC=1:4,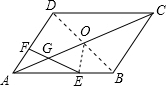
∴AG:AC=1:5,
∴AG:OG=2:5,
∵E是AB的中点,
又∵平行四边形ABCD中,O是BD的中点,
∴OE∥AD,OE=$\frac{1}{2}$AD,
∴AF:OE=AG:OG=2:5,
∴AD:AF=5:1,
∴$\frac{DF}{FA}$=4.
点评 此题主要考查平行线分线段成比例定理,能综合利用平行线分线段成比例、平行线的性质、比例的性质是解题的关键.

练习册系列答案
相关题目
13.若规定收入为“+”,那么支出40元表示( )
| A. | +40元 | B. | -40元 | C. | 0 | D. | +80元 |
 如图所示,直线AB和CD相交于点O,∠E0C=90°,∠COA+∠B0D=50°,求∠E0B的度数.
如图所示,直线AB和CD相交于点O,∠E0C=90°,∠COA+∠B0D=50°,求∠E0B的度数. 如图,在数轴上把下列各数表示出来,并用“<”连接各数.
如图,在数轴上把下列各数表示出来,并用“<”连接各数.