题目内容
11.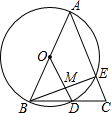 如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为8.
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为8.
分析 连接AD,由圆周角定理得出∠AEB=∠ADB=90°,由等腰三角形的性质得出BD=CD,由三角形中位线定理得出OD∥AC,CE=2MD=4,求出AE,再由勾股定理求出BE即可.
解答 解:连接AD,如图所示:
∵以AB为直径的⊙O与BC交于点D,
∴∠AEB=∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD∥AC,
∴BM=EM,
∴CE=2MD=4,
∴AE=AC-CE=6,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$;
故答案为:8.
点评 本题考查了圆周角定理、等腰三角形的性质、勾股定理、三角形中位线定理;熟练掌握圆周角定理,由三角形中位线定理求出CE是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.
为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.
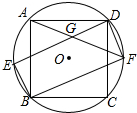 正方形ABCD内接于⊙O,如图所示,在劣弧$\widehat{AB}$上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
正方形ABCD内接于⊙O,如图所示,在劣弧$\widehat{AB}$上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: