题目内容
2. 为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.
为弘扬中华传统文化,某徽章设计公司设计了如图所示的一种新式徽章,每件的成本是50元,为了合理定价,先投放在某饰品店进行试销.试销发现,该徽章销售单价为100元时,每天的销售量是50件,且当销售单价每降低1元时,每天就可多售出5件.(1)如果该店每天要使该徽章的销售利润为4000元,则销售单价应定为多少元?
(2)该店每天该徽章的销售是否有最大利润?若有,请求出最大利润及销售单价,若没有,请说明理由.
分析 (1)利用每件商品利润×销量=总利润4000,得出关系式求出即可;
(2)把(1)中的二次函数解析式转化为顶点式方程,利用二次函数图象的性质进行解答.
解答 解:(1)设应将单价降低x元,则商店每天的销售量为(50+5x)件,
由题意得(50-x)(50+5x)=4000,
解得:x1=10,x2=30.
答:如果要使该企业每天的销售利润为4000元,应将销售单价应定为70元或90元;
(2)y=-5x2+800x-27500
=-5(x-80)2+4500
∵a=-5<0,
∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500;
即销售单价为80元时,每天的销售利润最大,最大利润是4500元.
点评 此题题考查二次函数的实际应用.为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14.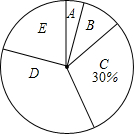 某学校为了解学生进行体育锻炼的情况,对某班学生每天的体育锻炼时间进行了统计,并绘制了以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
某学校为了解学生进行体育锻炼的情况,对某班学生每天的体育锻炼时间进行了统计,并绘制了以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
(1)求全班学生人数和m的值;
(2)该班学生的体育锻炼时间的中位数落在50≤x<60时间段;
(3)请你根据以上信息估计全校5000人中每天体育锻炼时间不少于50分钟的人数.
 某学校为了解学生进行体育锻炼的情况,对某班学生每天的体育锻炼时间进行了统计,并绘制了以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
某学校为了解学生进行体育锻炼的情况,对某班学生每天的体育锻炼时间进行了统计,并绘制了以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:| 分组 | 锻炼时间(分钟) | 频数 |
| A | 20≤x<30 | 2 |
| B | 30≤x<40 | 5 |
| C | 40≤x<50 | 15 |
| D | 50≤x<60 | m |
| E | 60≤x<70 | 10 |
(2)该班学生的体育锻炼时间的中位数落在50≤x<60时间段;
(3)请你根据以上信息估计全校5000人中每天体育锻炼时间不少于50分钟的人数.
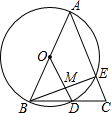 如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为8.
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为8.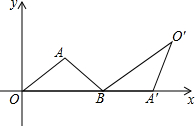 如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.
如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.