题目内容
1.在实数$\sqrt{4}$、$\sqrt{3}$、$\frac{1}{3}$、0.$\stackrel{•}{3}$、π、2.1234567891011121314…(自然数依次排列)、$\root{3}{-8}$中,无理数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据无理数的定义:无限不循环小数叫做无理数可得答案.
解答 解:无理数有$\sqrt{3}$,π,2.1234567891011121314…(自然数依次排列,共3个,
故选:B.
点评 此题主要考查了无理数,关键是掌握无理数定义.

练习册系列答案
相关题目
6.某班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|<3 |
(2)是否每次抽奖都会获奖,为什么?
13.已知2a=-5b,则$\frac{a}{b}$的值为( )
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | -$\frac{5}{2}$ |
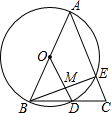 如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为8.
如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为8.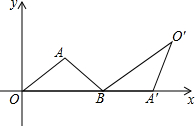 如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.
如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.