题目内容
 已知,如图所示,AB∥DC,∠1=∠2,∠3=∠4.
已知,如图所示,AB∥DC,∠1=∠2,∠3=∠4.(1)试判断AD与BE是否平行.
(2)写出推理过程.
考点:平行线的判定与性质
专题:
分析:根据平行可得到∠1+∠5=∠4=∠3=∠2+∠5,可证明AD∥BE.
解答: 解:
解:
(1)平行;
(2)证明如下:
∵AB∥CD,
∴∠1+∠5=∠4,
∵∠1=∠2,
∴∠2+∠5=∠4,
又∠3=∠4,
∴∠3=∠2+∠5,即∠3=∠DAC,
∴AD∥BE.
 解:
解:(1)平行;
(2)证明如下:
∵AB∥CD,
∴∠1+∠5=∠4,
∵∠1=∠2,
∴∠2+∠5=∠4,
又∠3=∠4,
∴∠3=∠2+∠5,即∠3=∠DAC,
∴AD∥BE.
点评:本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
当a<0时,|a-
|=( )
| 4a2 |
| A、a | B、-a | C、3a | D、-3a |
下列各因式分解中,结论正确的是( )
| A、x2-5x-6=(x-2)(x-3) |
| B、x2+x-6=(x+2)(x-3) |
| C、ax+ay+1=a(x+y)+1 |
| D、ma2b+mab2+ab=ab(ma+mb+1) |
 如图,OC⊥AB,∠AOE=∠COF,则OE、OF是什么位置关系?请说明理由.
如图,OC⊥AB,∠AOE=∠COF,则OE、OF是什么位置关系?请说明理由.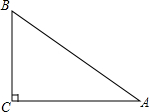 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用?
如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用? 如图,已知∠A+∠DBA=180°,∠3=58°,求∠4的度数.
如图,已知∠A+∠DBA=180°,∠3=58°,求∠4的度数. 如图,已知∠1=∠2,∠A=∠D,求证:∠C=∠F.
如图,已知∠1=∠2,∠A=∠D,求证:∠C=∠F. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).