题目内容
5.解应用题:一公司为了绿化道路环境,向某园林公司购买一批树苗,园林公司规定:如果购买树苗不超过100棵,每棵售价100元;如果购买树苗超过100棵,每增加2棵,所出售的这批树苗每棵售价均降低1元.如果每棵树苗最低售价不得少于80元,该公司最终向园林公司支付树苗款10800元,请问每棵树苗售价为多少元?此时该公司共购买了多少棵树苗?
分析 设当购买y棵树苗时,每棵树苗最低售价是80元,可得出当购买树苗140棵时,每棵树苗的价格刚好降为80元,设购买x棵树苗,分情况讨论,①当x≥140时,②当x<140时,分别表示出付款,再由该公司最终向园林公司支付树苗款10800元,可建立方程,解出后判断即可得出答案;
解答 解:设当购买y棵树苗时,每棵树苗最低售价是80元,
则100-$\frac{y-100}{2}$=80,解得y=140(棵)
设购买x棵树苗,付款为y,
①当x≥140时,y=80x,
则80x=10800,
解得:x=135;(不符合题意,舍去)
②当100<x<140时,每棵树的售价为(100-$\frac{x-100}{2}$),
y=(100-$\frac{x-100}{2}$)x=-$\frac{1}{2}$x2+150x,
则-$\frac{1}{2}$x2+150x=10800,
解得:x1=120,x2=180(舍去),
此时每棵树苗售价为90元,此时公司购进了120棵树苗.
答::每棵树苗的价格为90元,公司购进了120棵树苗.
点评 此题考查一元二次方程的实际运用,找出题目蕴含的数量关系,分类探讨得出答案即可.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
20.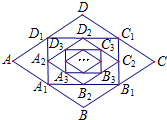 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{2}$ | D. | 5 |
17.下列根式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{9}$ | C. | $\sqrt{10}$ | D. | $\sqrt{12}$ |
 如图把一个转盘分成四等分依次标上数字1、2、3、4,若连续自由转动转盘两次,指针指向的数字分别记得a、b,作为点的横、纵坐标,
如图把一个转盘分成四等分依次标上数字1、2、3、4,若连续自由转动转盘两次,指针指向的数字分别记得a、b,作为点的横、纵坐标,