题目内容
10.下列等式不成立的是( )| A. | 6$\sqrt{2}$×$\sqrt{3}=6$$\sqrt{6}$ | B. | $\sqrt{8}$$÷\sqrt{2}=2$ | C. | $\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$ | D. | $\sqrt{8}-\sqrt{2}=2$ |
分析 原式各项计算得到结果,即可做出判断.
解答 解:A、原式=6$\sqrt{2×3}$=6$\sqrt{6}$,成立;
B、原式=$\sqrt{8÷2}$=$\sqrt{4}$=2,成立;
C、原式=$\frac{\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,成立;
D、原式=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$,不成立.
故选D.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
5.计算(-4)2×$\frac{1}{2}$的结果是( )
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
19.某商品经过两次连续降价,每件售价由原来的100元降到了64元.设平均每次降价的百分率为x,则下列方程中正确的是( )
| A. | 100(1+x)2=64 | B. | 64(1+x)2=100 | C. | 64(1-x)2=100 | D. | 100(1-x)2=64 |
20.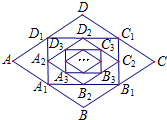 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….四边形A12B12C12D12的周长是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{2}$ | D. | 5 |
 如图,在△ABC中,∠A=60°,DE∥BC且BD平分∠ABC,CD平分∠ACB,∠EDB=20°,求∠ABC和∠ACB的度数.
如图,在△ABC中,∠A=60°,DE∥BC且BD平分∠ABC,CD平分∠ACB,∠EDB=20°,求∠ABC和∠ACB的度数.