题目内容
7.真情洒满校园,爱心传递温暖,西安市某中学校团委开展“关爱残疾儿童”爱心慈善捐款活动,学校团总支为了了解本校学生的捐款情况,随机抽取了若干名学生的捐款数进行了统计、并绘制成如图所示的不完整的扇形统计图: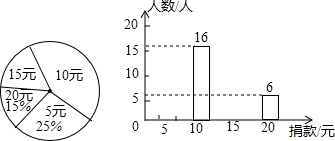
(1)将条形统计图补充完整;
(2)求抽取的这若干名同学捐款的平均数;
(3)若该校有600名学生参与捐款,据此估计捐款15元的学生人数约为多少?
分析 (1)利用捐款20元的6人除以所占的百分比求得总人数,进一步求得捐款5元和15元的人数,补全条形统计图即可;
(2)利用求平均数的方法得出答案即可;
(3)求得捐款15元的学生人数所占的百分比,乘学校人数即可得出答案.
解答 解:(1)6÷15%=40(人)
40×25%=10(人)
40-10-16-6=8(人)
条形统计图如下: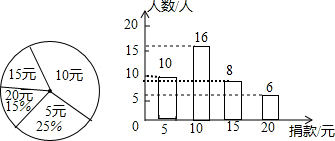
(2)抽取的这若干名同学捐款的平均数=(10×5+16×10+8×15+6×20)÷40=11.25(元);
(3)600×$\frac{8}{40}$=120(人)
答:估计捐款15元的学生人数约为120人.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
17.-$\frac{4}{5}$的相反数是( )
| A. | -$\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | -$\frac{5}{4}$ | D. | $\frac{4}{5}$ |
2. 如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
 如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )
如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )| A. | 25° | B. | 30° | C. | 40° | D. | 55° |
12.计算$\frac{{a}^{2}}{{b}^{3}}$$•\frac{2{b}^{2}}{3{a}^{2}}$的结果是( )
| A. | $\frac{2a}{3}$ | B. | $\frac{2b}{3}$ | C. | $\frac{2}{b}$ | D. | $\frac{2}{3b}$ |
17. 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 已知抛物线y=x2-2x-3
已知抛物线y=x2-2x-3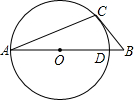 如图,AC是⊙O的弦,CB是⊙O的切线,C为切点,AB经过圆心与⊙O的交点为D,若∠B=50°,AD=10,则$\widehat{CD}$的长为$\frac{10}{9}$π.(结果保留π)
如图,AC是⊙O的弦,CB是⊙O的切线,C为切点,AB经过圆心与⊙O的交点为D,若∠B=50°,AD=10,则$\widehat{CD}$的长为$\frac{10}{9}$π.(结果保留π)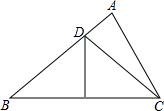 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,如果AD=3,BD=8,那么△ADC的周长为19.