Question

3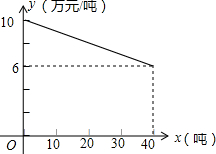．某工厂生产一种产品，当生产数量不超过40吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系式如图所示：
（1）求y关于x的函数解析式，并写出它的定义域；
（2）当生产这种产品的总成本为210万元时，求该产品的生产数量．（注：总成本=每吨的成本×生产数量）

Answer 1

分析 （1）直接利用待定系数法求出一次函数解析式进而得出答案；
（2）直接利用每吨的成本×生产吨数=总成本为210万元，进而得出等式求出答案．

解答 解：（1）设函数解析式为：y=kx+b，将（0，10），（40，6）分别代入y=kx+b得：
$\left\{\begin{array}{l}{10=b}\\{6=40k+b}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=10}\end{array}\right.$，
所以y=-$\frac{1}{10}$x+10（0≤x≤40）；

（2）由（-$\frac{1}{10}$x+10）x=210，
解得：x₁=30，x₂=70，
由于0≤x≤40，
所以x=30，
答：该产品的生产数量是30吨．

点评 此题主要考查了一次函数的应用，正确利用待定系数法求出一次函数解析式是解题关键．