题目内容
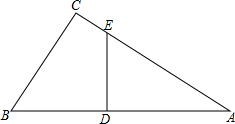 如图,在Rt△ABC中,∠C=90°,ED⊥AB.求证:∠AED=∠B.
如图,在Rt△ABC中,∠C=90°,ED⊥AB.求证:∠AED=∠B.证明:在Rt△ABC中,∠A+∠B=90°(根据是
在Rt△ADE中,∠A+∠AED=90°(根据是
所以∠AED=∠B(根据是
考点:直角三角形的性质
专题:证明题
分析:根据直角三角形两锐角互余可得出∠A+∠B=90°和∠A+∠AED=90°,再利用等量代换可得出结论.
解答:解:
在Rt△ABC和Rt△ADE中,由直角三角形两锐角互余可得到∠A+∠B=90°和∠A+∠AED=90°,
再利用等量代换可得到∠AED=∠B,
故答案为:直角三角形两锐角互余;直角三角形两锐角互余;等量代换.
在Rt△ABC和Rt△ADE中,由直角三角形两锐角互余可得到∠A+∠B=90°和∠A+∠AED=90°,
再利用等量代换可得到∠AED=∠B,
故答案为:直角三角形两锐角互余;直角三角形两锐角互余;等量代换.
点评:本题主要考查直角三角形的性质,掌握直角三角形两锐角互余是解题的关键.

练习册系列答案
相关题目
 小明从平面镜子中看到镜子对面钟表的像如图所示,这时的实际时间应是
小明从平面镜子中看到镜子对面钟表的像如图所示,这时的实际时间应是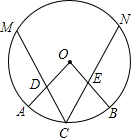 如图,在⊙O中,点C为
如图,在⊙O中,点C为
 已知正方形ABCD中点E,F分别在边AD,DC上,∠EBC=∠BEF,连接BD.下列结论:
已知正方形ABCD中点E,F分别在边AD,DC上,∠EBC=∠BEF,连接BD.下列结论: