题目内容
 已知正方形ABCD中点E,F分别在边AD,DC上,∠EBC=∠BEF,连接BD.下列结论:
已知正方形ABCD中点E,F分别在边AD,DC上,∠EBC=∠BEF,连接BD.下列结论:①EB平分∠AEF;②∠EBD=
| 1 |
| 2 |
| 1 |
| 8 |
其中正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质
专题:
分析:(1)根据内错角相等即可证明∠AEB=∠EBC,即可证明①正确;
(2)根据外角等于不相邻两内角和、对顶角相等的性质即可证明②正确;
(3)作BM⊥EF,连接BF,可证明EA=EM,FC=FM,即可解题;
(4)根据EF=AE+CF,只有E、F均为AD,CD中点时,△DEF面积有最大值;
(5)只有在∠ABE=30°时,才能证明△EDP∽△BDE,结论才成立,即可证明本选项错误.
(2)根据外角等于不相邻两内角和、对顶角相等的性质即可证明②正确;
(3)作BM⊥EF,连接BF,可证明EA=EM,FC=FM,即可解题;
(4)根据EF=AE+CF,只有E、F均为AD,CD中点时,△DEF面积有最大值;
(5)只有在∠ABE=30°时,才能证明△EDP∽△BDE,结论才成立,即可证明本选项错误.
解答:解:(1)∵AD∥BC,
∴∠AEB=∠EBC,
∵∠EBC=∠BEF,
∴∠AEB=∠BEF,
∴EB平分∠AEF;①正确;
(2)∵∠AEF=∠ADC+∠EFD,
∴∠AEB=
(90°+∠EFD),
∴∠BEF=
(90°+∠EFD),
∵∠BEF+∠EBP=∠EFD+∠BDC,
∴
(90°+∠EFD)+∠EBP=∠EFD+45°,
∴∠EBP=
∠EFD;②正确;
(3)作BM⊥EF,连接BF,
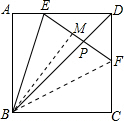
∵EB平分∠AEF,
∴BA=BM,
在RT△AEB和RT△MEB中,
,
∴RT△AEB和RT△MEB(HL)
∴EA=EM,
同理RT△BMF和RT△BCF,
∴FC=FM,
∴AE+CF=EF;③正确;
(4)∵EF=AE+CF,
∴只有在E、F均为AD,CD中点时,
△DEF面积有最大值S△DFP=
EF•DP(此时DP⊥EF)=
S正方形ABCD,∴④正确.
(5)只有△EDP∽△BDE时,DE2=DP•DB才成立,∴⑤不正确;
故选C.
∴∠AEB=∠EBC,
∵∠EBC=∠BEF,
∴∠AEB=∠BEF,
∴EB平分∠AEF;①正确;
(2)∵∠AEF=∠ADC+∠EFD,
∴∠AEB=
| 1 |
| 2 |
∴∠BEF=
| 1 |
| 2 |
∵∠BEF+∠EBP=∠EFD+∠BDC,
∴
| 1 |
| 2 |
∴∠EBP=
| 1 |
| 2 |
(3)作BM⊥EF,连接BF,

∵EB平分∠AEF,
∴BA=BM,
在RT△AEB和RT△MEB中,
|
∴RT△AEB和RT△MEB(HL)
∴EA=EM,
同理RT△BMF和RT△BCF,
∴FC=FM,
∴AE+CF=EF;③正确;
(4)∵EF=AE+CF,
∴只有在E、F均为AD,CD中点时,
△DEF面积有最大值S△DFP=
| 1 |
| 2 |
| 1 |
| 8 |
(5)只有△EDP∽△BDE时,DE2=DP•DB才成立,∴⑤不正确;
故选C.
点评:本题考查了正方形的性质,考查了全等三角形的判定,考查了全等三角形对应边相等的性质.

练习册系列答案
相关题目
 已知四边形EFGH相似于四边形KLMN,各边长如图所示,求∠E,∠G,∠N的度数以及x,y,z的值.
已知四边形EFGH相似于四边形KLMN,各边长如图所示,求∠E,∠G,∠N的度数以及x,y,z的值.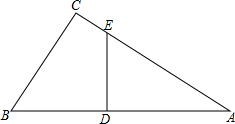 如图,在Rt△ABC中,∠C=90°,ED⊥AB.求证:∠AED=∠B.
如图,在Rt△ABC中,∠C=90°,ED⊥AB.求证:∠AED=∠B. 如图,AB是⊙O的直径,C、P是
如图,AB是⊙O的直径,C、P是
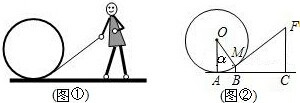 如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.
如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.