题目内容
已知x3+kx2+3除以x+3，其余数比被x+1除所得的余数少2，求k的值．
考点：整式的除法
专题：
分析：先分别得到x3+kx2+3除以x+3，x3+kx2+3除以x+1的余数，再根据x3+kx2+3除以x+3，其余数比被x+1除所得的余数少2，得到关于k的方程，求得k的值．
解答：解：（x3+kx2+3）÷（x+3）=x2+（k-3）x-3（k-3）…9k-24，
（x3+kx2+3）÷（x+1）=x2+（k-1）x-（k-1）…k十2，
∵x3+kx2+3除以x+3，其余数比被x+1除所得的余数少2，
∴9k-24+2=2+k，
解得k=3．
故k的值是3．
（x3+kx2+3）÷（x+1）=x2+（k-1）x-（k-1）…k十2，
∵x3+kx2+3除以x+3，其余数比被x+1除所得的余数少2，
∴9k-24+2=2+k，
解得k=3．
故k的值是3．
点评：考查了整式的除法，本题关键是得到两个除法算式的余数．
练习册系列答案
相关题目
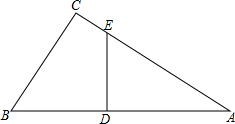如图，在Rt△ABC中，∠C=90°，ED⊥AB．求证：∠AED=∠B．
如图，在正方形ABCD中，AB=1，以边AB为直径向正方形内作半圆，自点C、D分别作半圆的切线CE、DF，则线段EF的长为多少？