题目内容
13.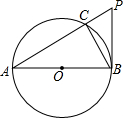 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
分析 (1)根据已知条件得到∠ACB=∠ABP=90°,根据余角的性质即可得到结论;
(2)根据相似三角形的判定和性质即可得到结论;
(3)根据三角函数的定义即可得到结论.
解答  解:(1)∵AB是⊙O的直径,PB与⊙O相切于点B,
解:(1)∵AB是⊙O的直径,PB与⊙O相切于点B,
∴∠ACB=∠ABP=90°,
∴∠A+∠ABC=∠ABC+∠CBP=90°,
∴∠BAC=∠CBP;
(2)∵∠PCB=∠ABP=90°,
∠P=∠P,
∴△ABP∽△BCP,
∴$\frac{PB}{AP}=\frac{PC}{PB}$,
∴PB2=PC•PA;
(3)∵PB2=PC•PA,AC=6,CP=3,
∴PB2=9×3=27,
∴PB=3$\sqrt{3}$,
∴sin∠PAB=$\frac{PB}{AP}$=$\frac{3\sqrt{3}}{9}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定和性质,切线的性质,圆周角定理,三角函数的定义,正确的识别图形是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
3.微信根据移动ID所带来的数据,发布了“微信用户春节迁徙数据报告”,该报告显示,2016年1月24日春运首日至2月4日期间,人口流入最多的省份约有3 130 000微信用户在春节期间返乡.3 130 000用科学记数法可表示为( )
| A. | 3.13×102 | B. | 313×104 | C. | 3.13×105 | D. | 3.13×106 |
1.下列事件中,是必然事件的为( )
| A. | 明天会下雨 | B. | 打开电视机,正在播放动画片 | ||
| C. | 三角形内角和为180° | D. | 经过一个路口,信号灯刚好是红灯 |
2.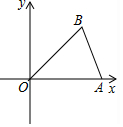 如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
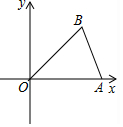 如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )| A. | 向左平移1个单位,再向下平移1个单位 | |
| B. | 向左平移(2$\sqrt{2}$-1)个单位,再向上平移1个单位 | |
| C. | 向右平移$\sqrt{2}$个单位,再向上平移1个单位 | |
| D. | 向右平移1个单位,再向上平移1个单位 |
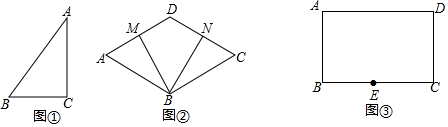
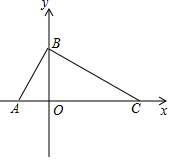 如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.
如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.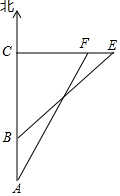 钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)
钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)