题目内容
3.先化简$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$÷($\frac{x-1}{x+1}$-x+1),然后从-$\sqrt{5}$<x<$\sqrt{5}$的范围内选取一个合适的整数作为x的值代入求值.分析 根据分式的减法和除法可以化简题目中的式子,然后在-$\sqrt{5}$<x<$\sqrt{5}$中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.
解答 解:$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$÷($\frac{x-1}{x+1}$-x+1)
=$\frac{(x-1)^{2}}{(x+1)(x-1)}÷\frac{x-1-(x-1)(x+1)}{x+1}$
=$\frac{x-1}{x+1}•\frac{x+1}{x-1-{x}^{2}+1}$
=$\frac{x-1}{-x(x-1)}$
=$-\frac{1}{x}$,
∵-$\sqrt{5}$<x<$\sqrt{5}$且x+1≠0,x-1≠0,x≠0,x是整数,
∴x=-2时,原式=-$\frac{1}{-2}=\frac{1}{2}$.
点评 本题考查分式的化简求值、估算无理数的大小,解答本题的关键是明确分式化简求值的方法,注意取得的x的值必须使得原分式有意义.

练习册系列答案
相关题目
13.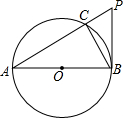 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
14.某单位组织职工开展植树活动,植树量与人数之间关系如图,下列说法不正确的是( )
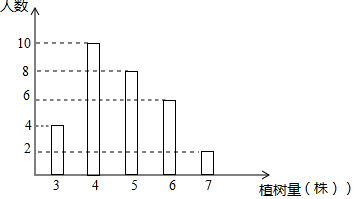

| A. | 参加本次植树活动共有30人 | B. | 每人植树量的众数是4棵 | ||
| C. | 每人植树量的中位数是5棵 | D. | 每人植树量的平均数是5棵 |
15.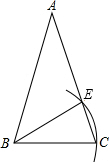 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )| A. | AE=EC | B. | AE=BE | C. | ∠EBC=∠BAC | D. | ∠EBC=∠ABE |
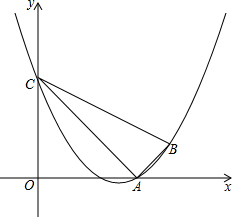 如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.
如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.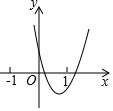 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系中的大致图象是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系中的大致图象是( )


